AHPとは
AHPとはAnalytic Hierarchy Process(階層的意思決定法)と呼ばれる理論です。その計算はある目的に対して代替案が複数ある時どの代替案が最も良いか数値化して評価する方法で、計算の特徴は人が考える評価点をバランスよく数値化することができます。
今回の記事はAHPの計算理論について紹介しようと思います!
まずはその構造を紹介します。階層的意思決定法という名前の通りで判断したい内容を階層に分解します。
見た目はこんな感じです。
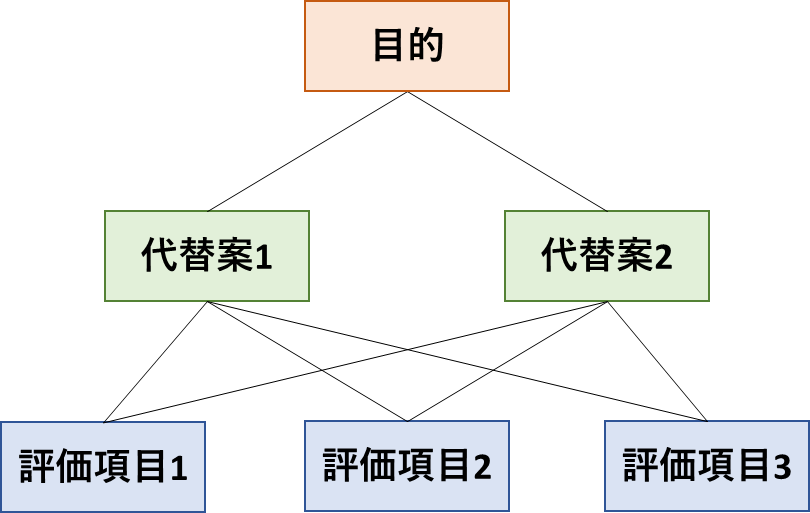
この図の
➀「評価項目」ごとの重要度を数値化
➁「代替案」に対する「評価項目」の得点を付ける
③「目的」に対する「代替案」の得点が計算
のステップで代替案の得点を数値化しもっとも良い代替案を決定できます。
概念だとイメージしにくいのでもう少しイメージを具体化します。
AHPのイメージ
AHPの計算の考え方のベースは一対比較を行いその感覚のずれを調整することです。
人の感性では複数の評価項目があるとどっちの方がより重要なのか悩んでしまいます。
引っ越し先を考える例で考えてみます。
代替案が「物件A」, 「物件B」、その評価項目を「価格の安さ」, 「広さ」, 「場所の良さ」としましょう。
「価格の安さ」と「広さ」で比べると「価格が安さ」よりも「広さ」方が大事だと思っています。
「価格の安さ」と「場所の良さ」で比べると「価格の安さ」が「場所の良さ」よりも大事だとしましょう。
この時、評価項目は
$$
広さ>価格の安さ>場所の良さ
$$
の順に大事なことが分かります。
ここで2つの物件は表のようなイメージです。
| 物件A | 物件B | |
| 広さ | 〇 | △ |
| 価格の安さ | △ | 〇 |
| 場所の良さ | △ | 〇 |
一番大事な「広さ」については物件Aの方が良い一方で他の2項目は物件Bの方が良いという状態で、どちらを選んだ方がより幸せかどうかと思うとなかなか決めきれなくなってしまいますよね。。
また、
「広さ」は「価格の安さ」よりも2倍大事!
「価格の安さ」は「場所の良さ」よりも2倍大事!
と思っていた場合、
「広さ」は「場所の良さ」よりも4倍大事!
とならないと矛盾していますよね。人の感性はあいまいで、
実際に評価項目が4つ、5つと増えてくると感覚ではほぼ100%矛盾なしの重さは決められません。
それらを調整してくれるのがAHPです。
➀「評価項目」はどの順番でどれだけの重要度を持っているのか
➁「選択肢」は各「評価項目」ごとでどれが優れているのか
この2点を数値化し、かつ、矛盾を調整できる計算です。
この調整方法を計算理論で確認していきます。
AHPの計算理論
ここからは計算方法について確認してみます。
評価項目の重要度を$$W_n$$とします。
今回の例ではこんな感じです
$$広さ = W_1$$
$$価格の安さ = W_2$$
$$場所の良さ = W_3$$
重要度を割合で表してみると、
$$\frac{価格の安さ}{広さ} = \frac{W_2}{W_1}$$
となります。この関係すべてを表でまとめてみるとこうなります。
| 評価項目の重さ | 広さ | 価格の安さ | 場所の良さ |
| 広さ | $$\frac{W_1}{W_1}$$ | $$\frac{W_1}{W_2}$$ | $$\frac{W_1}{W_3}$$ |
| 価格の安さ | $$\frac{W_2}{W_1}$$ | $$\frac{W_2}{W_2}$$ | $$\frac{W_3}{W_3}$$ |
| 場所の良さ | $$\frac{W_3}{W_1}$$ | $$\frac{W_3}{W_2}$$ | $$\frac{W_3}{W_3}$$ |
この表の重さはどう考えるかというと一対比較で順々に考えていきます。
一対比較は次のように進めます。
「広さ」と「価格の安さ」ではどちらがどれくらい大事か?
「広さ」と「場所の良さ」ではどちらがどれくらい大事か?
「価格の安さ」と「場所の良さ」ではどっちがどれくらい大事か?
と各項目を一つずつ比べて全ての評価項目を一対一で比べて数値を埋めていきます。
綺麗な表ができると行列計算で上手いこと計算ができそうですね。
今回はまさにそうです。
$$
A=\begin{bmatrix}
\frac{W_1}{W_1} & \frac{W_1}{W_2} & \frac{W_1}{W_3} \\
\frac{W_2}{W_1} & \frac{W_2}{W_2} & \frac{W_2}{W_3} \\
\frac{W_3}{W_1} & \frac{W_3}{W_2} & \frac{W_3}{W_3}
\end{bmatrix}
$$
とAを置いてみて固有値を考えます。すると見た目はこうなりますね。
$$
\begin{bmatrix}
\frac{W_1}{W_1} & \frac{W_1}{W_2} & \frac{W_1}{W_3} \\
\frac{W_2}{W_1} & \frac{W_2}{W_2} & \frac{W_2}{W_3} \\
\frac{W_3}{W_1} & \frac{W_3}{W_2} & \frac{W_3}{W_3}
\end{bmatrix}
\begin{bmatrix}
W_1 \\
W_2 \\
W_3
\end{bmatrix}
= \lambda
\begin{bmatrix}
W_1 \\
W_2 \\
W_3
\end{bmatrix}
$$
いきなり式が出てきたように感じますがゆっくり考えてみてください。
Aの一行目と固有ベクトルの積を考えてみましょう。
Aの分母は右に\(W_1, W_2, W_3\)と進むため、後ろの列ベクトルと綺麗に
約分されて
$$
\begin{bmatrix}
\frac{W_1}{W_1} & \frac{W_1}{W_2} & \frac{W_1}{W_3}
\end{bmatrix}
\begin{bmatrix}
W_1 \\
W_2 \\
W_3
\end{bmatrix}
=3W_1
$$
と計算でき、掛けたベクトルと同じベクトルが出力されるのがわかると思います。
3行とも同様の結果が得られるため結果の固有ベクトルにまとめると
この時λは3(ベクトルの長さ)になりますね。
$$
3
\begin{bmatrix}
W_1 \\
W_2 \\
W_3
\end{bmatrix}
$$
ここまで見えてくると理論はOKです!(整合度については後日書きます)
➀それぞれの評価項目を1対1の割合で比較し重さを順に考える
➁重さに矛盾があるところを理論値で補正
のステップでシステマティックに調整された真の重み付けが分かるのです!
計算例
先ほどの例を少し数値にしてみましょう。
| 評価項目の重さ | 広さ | 価格の安さ | 場所の良さ |
| 広さ | $$1$$ | $$\frac{1}{2}$$ | $$\frac{1}{3}$$ |
| 価格の安さ | $$2$$ | $$1$$ | $$\frac{1}{2}$$ |
| 場所の良さ | $$3$$ | $$2$$ | $$1$$ |
この表から固有値を計算し
$$
\begin{bmatrix}
0.164 \\
0.405 \\
1.00
\end{bmatrix}
$$
ウェイトの合計を1に調整すると
$$
\begin{bmatrix}
広さ \\
価格の安さ \\
場所の良さ
\end{bmatrix}
=
\begin{bmatrix}
0.105 \\
0.258 \\
0.637
\end{bmatrix}
$$
となります。
代替案も同様にウェイトを考えます。各評価項目それぞれに対して考えます。
代替案は「東京物件」,「神奈川物件」,「埼玉物件」の3つとして考えます。
広さに対して代替案の良し悪しを考えます。以下の表のウェイトになったとしましょう。
| 広さ | 東京物件 | 神奈川物件 | 埼玉物件 |
| 東京物件 | $$1$$ | $$\frac{1}{3}$$ | $$\frac{1}{5}$$ |
| 神奈川物件 | $$3$$ | $$1$$ | $$\frac{1}{2}$$ |
| 埼玉物件 | $$5$$ | $$2$$ | $$1$$ |
「広さ」に対して以下のような得点になります。
$$
\begin{bmatrix}
東京物件 \\
神奈川物件 \\
埼玉物件
\end{bmatrix}
=
\begin{bmatrix}
0.109 \\
0.309 \\
0.582
\end{bmatrix}
$$
同様にして「価格の安さ」、「場所の良さ」についても計算したとしましょう。
この結果に加えて先ほどの評価項目と掛け合わせ総合得点を表にまとめます。
| 広さ | 価格の安さ | 場所の良さ | 総合得点 | |
| 東京 | $$0.109$$ | $$0.550$$ | $$0.731$$ | $$0.619$$ |
| 神奈川 | $$0.309$$ | $$0.240$$ | $$0.188$$ | $$0.214$$ |
| 埼玉 | $$0.582$$ | $$0.210$$ | $$0.081$$ | $$0.167$$ |
この結果から総合得点の最も高い引っ越し先は東京が良いとわかります。
まだまだ捕捉したい点はあるのですが、今回はここまでにします。
後日、整合度と合わせてAHPの補足をしていきます。
それもまとめられたらAHPを計算できるページを作りたいと思います。
ここまでありがとうございました。

コメント